fft.scala // Jump To …

ack.html automata.html dslapi.html dynvar.html eval.html fft.html index.html query.html regex.html scanner.html scannerlib.html shonan.html start.html stencil.html utils.html

Fast Fourier Transform (FFT)

Outline:

Staging FFT

We consider staging a fast fourier transform (FFT) algorithm. A staged FFT, implemented in MetaOCaml, has been presented by Kiselyov et al. [EMSOFT'04]. Their work is a very good example for how staging allows to transform a simple, unoptimized algorithm into an efficient program generator. Achieving this in the context of MetaOCaml, however, required restructuring the program into monadic style and adding a front-end layer for performing symbolic rewritings. Using our approach of just adding Rep types, we can go from the naive textbook-algorithm to the staged version by changing literally two lines of code:

trait FFT { this: Arith with Trig =>
  case class Complex(re: Rep[Double], im: Rep[Double])
  ...
}

All that is needed is adding the self-type annotation to import arithmetic and trigonometric operations and changing the type of the real and imaginary components of complex numbers from Double to Rep[Double].

See the trait FFT. Only the real and imaginary components of complex numbers need to be staged.

Merely changing the types will not provide us with the desired optimizations yet. We will see how we can add the transformations described by Kiselyov et al. to generate the same fixed-size FFT code, corresponding to the famous FFT butterfly networks. Despite the seemingly naive algorithm, this staged code is free of branches, intermediate data structures and redundant computations. The important point here is that we can add these transformations without any further changes to the code, just by mixing in the trait FFT with a few others, extending the generic implementation with FFT-specific optimizations.

Implementing Optimizations

As already discussed, some profitable optimizations are very generic (CSE, DCE, etc), whereas others are specific to the actual program. In the FFT case, Kiselyov et al. describe a number of rewritings that are particularly effective for the patterns of code generated by the FFT algorithm but not as much for other programs.

What we want to achieve again is modularity, such that optimizations can be combined in a way that is most useful for a given task. This can be achieved by overriding smart constructors, as shown by trait ArithExpOptFFT. Note that the use of x*y within the body of infix_* will apply the optimization recursively.

Running the Generated Code

Extending the FFT component with explicit compilation. See trait FFTC.

Using the staged FFT implementation as part of some larger Scala program is straightforward but requires us to interface the generic algorithm with a concrete data representation. The algorithm in FFT expects an array of Complex objects as input, each of which contains fields of type Rep[Double]. The algorithm itself has no notion of staged arrays but uses arrays only in the generator stage, which means that it is agnostic to how data is stored. The enclosing program, however, will store arrays of complex numbers in some native format which we will need to feed into the algorithm. A simple choice of representation is to use Array[Double] with the complex numbers flattened into adjacent slots. When applying compile, we will thus receive input of type Rep[Array[Double]]. We can extend trait FFT to FFTC to obtain compiled FFT implementations that realize the necessary data interface for a fixed input size.

We can then define code that creates and uses compiled FFT “codelets” by extending FFTC. See the trait TestFFTC.

Constructing an instance of this subtrait (mixed in with the appropriate LMS traits) will execute the embedded code:

val OP: TestFFC = new TestFFTC with FFTCExp

We can also use the compiled methods from outside the object:

OP.fft4(Array(1.0,0.0, 1.0,0.0, 2.0,0.0, 2.0,0.0))
$\hookrightarrow$ Array(6.0,0.0,-1.0,1.0,0.0,0.0,-1.0,-1.0)

Providing an explicit type in the definition val OP: TestFFC = ... ensures that the internal representation is not accessible from the outside, only the members defined by TestFFC.

Full Code

Note that the full code does not make use of the tutorial API. It puts together from scratch all the parts of the LMS framework it needs.

package scala.lms.tutorial.fft
import scala.lms.tutorial._

import scala.reflect.SourceContext
import java.io.PrintWriter

import scala.lms.common._
import scala.lms.internal._
import scala.reflect._

Arith

Instead of using the LMS common arithmetic package, we create one from scratch.

trait LiftArith {
  this: Arith =>

  implicit def numericToRep[T:Numeric:Typ](x: T) = unit(x)
}

trait Arith extends Base with LiftArith {
  implicit def intTyp: Typ[Int]
  implicit def doubleTyp: Typ[Double]

  implicit def intToArithOps(i: Int): arithOps = new arithOps(unit(i))
  implicit def intToRepDbl(i: Int) : Rep[Double] = unit(i)

  class arithOps(x: Rep[Double]){
    def +(y: Rep[Double]) = infix_+(x,y)
    def -(y: Rep[Double]) = infix_-(x,y)
    def *(y: Rep[Double]) = infix_*(x,y)
    def /(y: Rep[Double]) = infix_/(x,y)
  }

  def infix_+(x: Rep[Double], y: Rep[Double])(implicit pos: SourceContext): Rep[Double]
  def infix_-(x: Rep[Double], y: Rep[Double])(implicit pos: SourceContext): Rep[Double]
  def infix_*(x: Rep[Double], y: Rep[Double])(implicit pos: SourceContext): Rep[Double]
  def infix_/(x: Rep[Double], y: Rep[Double])(implicit pos: SourceContext): Rep[Double]
}

trait ArithExp extends Arith with BaseExp {
  implicit def intTyp: Typ[Int] = manifestTyp
  implicit def doubleTyp: Typ[Double] = manifestTyp

  case class Plus(x: Exp[Double], y: Exp[Double]) extends Def[Double]
  case class Minus(x: Exp[Double], y: Exp[Double]) extends Def[Double]
  case class Times(x: Exp[Double], y: Exp[Double]) extends Def[Double]
  case class Div(x: Exp[Double], y: Exp[Double]) extends Def[Double]

  def infix_+(x: Exp[Double], y: Exp[Double])(implicit pos: SourceContext) = Plus(x, y)
  def infix_-(x: Exp[Double], y: Exp[Double])(implicit pos: SourceContext) = Minus(x, y)
  def infix_*(x: Exp[Double], y: Exp[Double])(implicit pos: SourceContext) = Times(x, y)
  def infix_/(x: Exp[Double], y: Exp[Double])(implicit pos: SourceContext) = Div(x, y)

  override def mirror[A:Typ](e: Def[A], f: Transformer)(implicit pos: SourceContext): Exp[A] =
    (e match {
      case Plus(x,y) => f(x) + f(y)
      case Minus(x,y) => f(x) - f(y)
      case Times(x,y) => f(x) * f(y)
      case Div(x,y) => f(x) / f(y)
      case _ => super.mirror(e,f)
    }).asInstanceOf[Exp[A]]
}

trait ArithExpOpt extends ArithExp {

  override def infix_+(x: Exp[Double], y: Exp[Double])(implicit pos: SourceContext) =
    (x, y) match {
      case (Const(x), Const(y)) => Const(x + y)
      case (x, Const(0.0) | Const(-0.0)) => x
      case (Const(0.0) | Const(-0.0), y) => y
      case _ => super.infix_+(x, y)
    }

  override def infix_-(x: Exp[Double], y: Exp[Double])(implicit pos: SourceContext) =
    (x, y) match {
      case (Const(x), Const(y)) => Const(x - y)
      case (x, Const(0.0) | Const(-0.0)) => x
      case _ => super.infix_-(x, y)
    }

  override def infix_*(x: Exp[Double], y: Exp[Double])(implicit pos: SourceContext) =
    (x, y) match {
      case (Const(x), Const(y)) => Const(x * y)
      case (x, Const(1.0)) => x
      case (Const(1.0), y) => y
      case (x, Const(0.0) | Const(-0.0)) => Const(0.0)
      case (Const(0.0) | Const(-0.0), y) => Const(0.0)
      case _ => super.infix_*(x, y)
    }

  override def infix_/(x: Exp[Double], y: Exp[Double])(implicit pos: SourceContext) =
    (x, y) match {
      case (Const(x), Const(y)) => Const(x / y)
      case (x, Const(1.0)) => x
      case _ => super.infix_/(x, y)
    }
}

trait ScalaGenArith extends ScalaGenBase {
  val IR: ArithExp
  import IR._

  override def emitNode(sym: Sym[Any], rhs: Def[Any]) = rhs match {
    case Plus(a,b) =>  emitValDef(sym, "" + quote(a) + "+" + quote(b))
    case Minus(a,b) => emitValDef(sym, "" + quote(a) + "-" + quote(b))
    case Times(a,b) => emitValDef(sym, "" + quote(a) + "*" + quote(b))
    case Div(a,b) =>   emitValDef(sym, "" + quote(a) + "/" + quote(b))
    case _ => super.emitNode(sym, rhs)
  }
}

Trig

We also create a trigonometry package.

trait Trig extends Base {
  def sin(x: Rep[Double]): Rep[Double]
  def cos(x: Rep[Double]): Rep[Double]
}

trait TrigExp extends Trig with BaseExp {
  implicit def doubleTyp: Typ[Double]

  case class Sin(x: Exp[Double]) extends Def[Double]
  case class Cos(x: Exp[Double]) extends Def[Double]

  def sin(x: Exp[Double]) = Sin(x)
  def cos(x: Exp[Double]) = Cos(x)
}

trait TrigExpOpt extends TrigExp {
  override def sin(x: Exp[Double]) = x match {
    case Const(x) => unit(math.sin(x))
    case _ => super.sin(x)
  }
  override def cos(x: Exp[Double]) = x match {
    case Const(x) => unit(math.cos(x))
    case _ => super.cos(x)
  }
}

We don't need sin and cos in the generated code for our purposes…

trait ScalaGenTrig {
  // ...
}

Arrays

We create a minimal package for arrays.

We use the effect system of LMS to ensure updates are recorded.

trait Arrays extends Base {
  implicit def arrayTyp[T:Typ]: Typ[Array[T]]

  implicit class ArrayOps[T:Typ](x: Rep[Array[T]]) {
    def apply(i: Int) = arrayApply(x, i)
    def update(i: Int, v: Rep[T]) = arrayUpdate(x,i, v)
  }

  def arrayApply[T:Typ](x: Rep[Array[T]], i:Int): Rep[T]
  def arrayUpdate[T:Typ](x: Rep[Array[T]], i:Int, v:Rep[T]): Rep[Unit]

The function updateArray is staging-time. It updates a dynamic array given a static array by an unrolled loop.

  def updateArray[T:Typ](x: Rep[Array[T]], v: Array[Rep[T]]): Rep[Array[T]] = {
    for (i <- 0 until v.length)
      arrayUpdate(x, i, v(i))
    x
  }

  def mutable[T:Typ](x: Rep[T]): Unit
}

trait ArraysExp extends Arrays with EffectExp {
  implicit def arrayTyp[T:Typ]: Typ[Array[T]] = typ[T].arrayTyp

  case class ArrayApply[T:Typ](x:Rep[Array[T]], i:Int) extends Def[T]
  case class ArrayUpdate[T:Typ](x:Rep[Array[T]], i:Int, v: Rep[T]) extends Def[Unit]

  def arrayApply[T:Typ](x: Rep[Array[T]], i:Int) = ArrayApply(x, i)
  def arrayUpdate[T:Typ](x: Rep[Array[T]], i:Int, v: Rep[T]) = reflectWrite(x)(ArrayUpdate(x,i,v))

  def mutable[T:Typ](x: Rep[T]): Unit = reflectMutableSym(x.asInstanceOf[Sym[T]])
}

trait ArraysExpOpt extends ArraysExp {
  // ...
}

trait ScalaGenArrays extends ScalaGenBase {
  val IR: ArraysExp
  import IR._

  override def emitNode(sym: Sym[Any], rhs: Def[Any]) = rhs match {
    case ArrayApply(x,i) => emitValDef(sym, src"$x(${i.toString})")
    case ArrayUpdate(x,i,v) => emitValDef(sym, src"$x(${i.toString})=$v")
    case _ => super.emitNode(sym, rhs)
  }
}

Disable Optimizations

We can disable default LMS optimizations just by mixing in these traits. This will allow us to compare the unoptimized and optimized FFT code.

trait DisableCSE extends Expressions {
  override def findDefinition[T: Typ](d: Def[T]) = None
}

trait DisableDCE extends GraphTraversal {
  import IR._
  override def buildScheduleForResult(start: Any, sort: Boolean = true): List[Stm] = globalDefs
}

FFT

Finally, here is the FFT class. Notice that the code looks standard, except for the Reps in the real and imaginary fields of the Complex class.

trait FFT { this: Arith with Trig =>
  case class Complex(re: Rep[Double], im: Rep[Double]) {
    def +(that: Complex) = Complex(this.re + that.re, this.im + that.im)
    def -(that: Complex) = Complex(this.re - that.re, this.im - that.im)
    def *(that: Complex) = Complex(this.re * that.re - this.im * that.im,
                                   this.re * that.im + this.im * that.re)
  }
  def omega(k: Int, N: Int): Complex = {
    val kth = -2.0 * k * math.Pi / N
    Complex(cos(kth), sin(kth))
  }
  def fft(xs: Array[Complex]): Array[Complex] =
    if (xs.length == 1) xs
    else {
      val N = xs.length // assume it's a power of two
      val (even0, odd0) = splitEvenOdd(xs)
      val (even1, odd1) = (fft(even0), fft(odd0))
      val (even2, odd2) = (even1 zip odd1 zipWithIndex) map {
        case ((x, y), k) =>
          val z = omega(k, N) * y
          (x + z, x - z)
      } unzip;
      even2 ++ odd2
    }

  // helpers
  def splitEvenOdd[T](xs: List[T]): (List[T], List[T]) = (xs: @unchecked) match {
    case e :: o :: xt =>
      val (es, os) = splitEvenOdd(xt)
      ((e :: es), (o :: os))
    case Nil => (Nil, Nil)
  }
  def splitEvenOdd[T:ClassTag](xs: Array[T]): (Array[T], Array[T]) = {
    val r = splitEvenOdd[T](xs.toList)
    (r._1.toArray, r._2.toArray)
  }

  def mergeEvenOdd[T](even: List[T], odd: List[T]): List[T] = ((even, odd): @unchecked) match {
    case (Nil, Nil) =>
      Nil
    case ((e :: es), (o :: os)) =>
      e :: (o :: mergeEvenOdd(es, os))
  }
  def mergeEvenOdd[T:ClassTag](even: Array[T], odd: Array[T]): Array[T] =
    mergeEvenOdd(even.toList, odd.toList).toArray
}

trait ArithExpOptFFT extends ArithExpOpt {
  override def infix_+(x: Exp[Double], y: Exp[Double])(implicit pos: SourceContext) =
    (x, y) match {
      case (x, Def(Minus(Const(0.0) | Const(-0.0), y))) => infix_-(x, y)
      case _ => super.infix_+(x, y)
    }

  override def infix_-(x: Exp[Double], y: Exp[Double])(implicit pos: SourceContext) =
    (x, y) match {
      case (x, Def(Minus(Const(0.0) | Const(-0.0), y))) => infix_+(x, y)
      case _ => super.infix_-(x, y)
    }

  override def infix_*(x: Exp[Double], y: Exp[Double])(implicit pos: SourceContext) =
    (x, y) match {
      case (x, Const(-1.0)) => infix_-(0.0, x)
      case (Const(-1.0), y) => infix_-(0.0, y)
      case _ => super.infix_*(x, y)
    }
}

trait TrigExpOptFFT extends TrigExpOpt {
  override def cos(x: Exp[Double]) = x match {
    case Const(x) if { val z = x / math.Pi / 0.5; z != 0 && z == z.toInt } => Const(0.0)
    case _ => super.cos(x)
  }
}

trait FlatResult extends BaseExp { // just to make dot output nicer
  case class Result[T](x: Any) extends Def[T]
  def result[T:Typ](x: Any): Exp[T] = {
    val r = x match {
      case (a: Array[_]) => a.toList
      case _ => x
    }
    toAtom(Result[T](r))
  }
}

trait ScalaGenFlat extends ScalaGenEffect {
  val IR: Expressions with Effects
  import IR._
  override def getBlockResultFull[T](x: Block[T]): Exp[T] = getBlockResult(x)
  override def reifyBlock[T:Typ](x: =>Exp[T]): Block[T] = IR.reifyEffects(x)
  override def traverseBlock[A](block: Block[A]): Unit = {
    buildScheduleForResult(block) foreach traverseStm
  }
}

trait FFTC { this: FFT with Arith with Arrays with Compile =>
  def fftc(size: Int) = compile { input: Rep[Array[Double]] =>
    mutable(input)
    val arg = Array.tabulate(size){i =>
      Complex(input(2*i), input(2*i+1))
    }
    val res = fft(arg)
    updateArray(input, res.flatMap {
      case Complex(re,im) => Array(re,im)
    })
  }

  // This is because we're using an Array of Rep.
  implicit def repClassTag[T:ClassTag]: ClassTag[Rep[T]]
}

trait FFTCExp extends FFTC with FFT with ArithExpOptFFT with TrigExpOptFFT with ArraysExpOpt with CompileScala { self =>
  val IR: self.type = self
  val codegen = new ScalaGenFFT {
    val IR: self.type = self
  }

  def repClassTag[T:ClassTag]: ClassTag[Rep[T]] = classTag
}

trait ScalaGenFFT extends ScalaGenFlat with ScalaGenArith with ScalaGenTrig with ScalaGenArrays {
  val IR: FFTCExp
}

trait TestFFTC { this: FFTC =>
  lazy val fft4: Array[Double] => Array[Double] = fftc(4)
  lazy val fft8: Array[Double] => Array[Double] = fftc(8)

  // embedded code using fft4, fft8, ...
}

Tests

class TestFFT extends TutorialFunSuite {

  val under = "fft"

  test("1") {
    checkOut("1", "txt", {
      val o = new FFT with ArithExp with TrigExpOpt with FlatResult with DisableCSE
      import o._

      val r = result[Unit](fft(Array.tabulate(4)(_ => Complex(fresh[Double], fresh[Double]))))
      println(globalDefs.mkString("\n"))
      println(r)

      val p = new ExportGraph with DisableDCE { val IR: o.type = o }
      p.emitDepGraph(r, prefix+under+"1.dot", true)
    })
  }

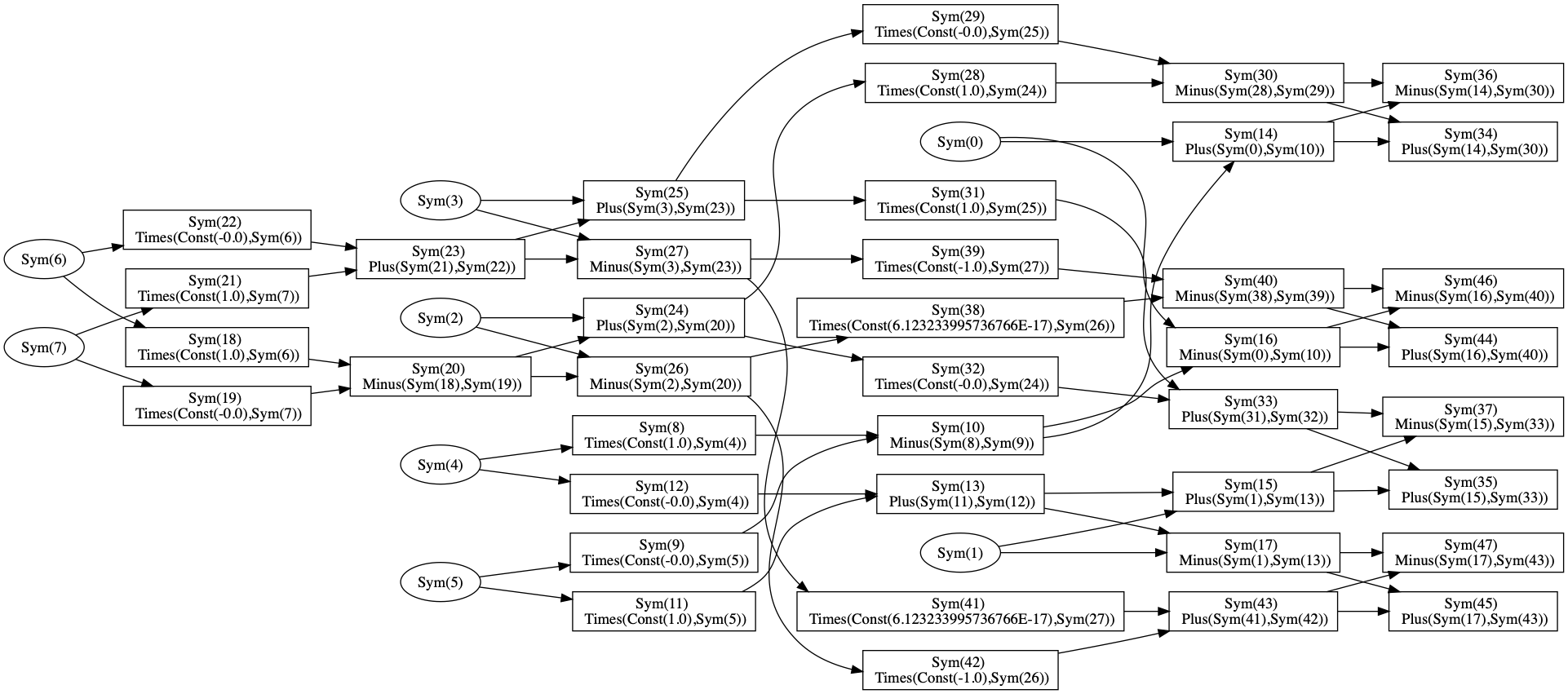Computation graph for size-4 FFT, unoptimized.

  test("2") {
    checkOut("2", "txt", {
      val o = new FFT with ArithExpOptFFT with TrigExpOptFFT with FlatResult
      import o._

      val r = result[Unit](fft(Array.tabulate(4)(_ => Complex(fresh[Double], fresh[Double]))))
      println(globalDefs.mkString("\n"))
      println(r)

      val p = new ExportGraph { val IR: o.type = o }
      p.emitDepGraph(r, prefix+under+"2.dot", true)
    })
  }

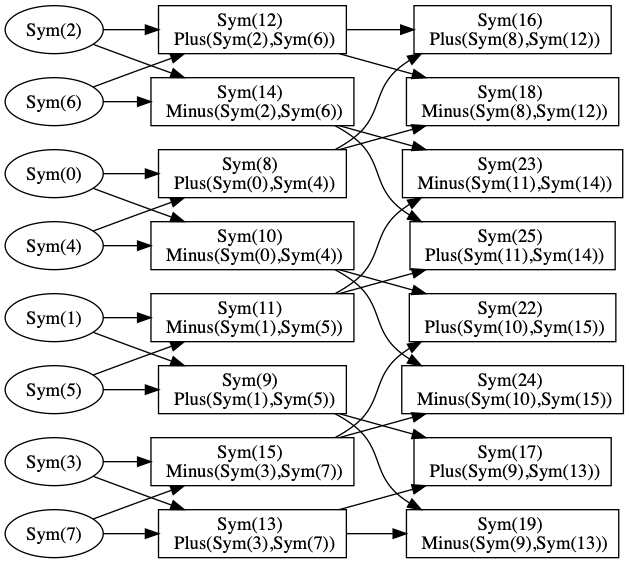Computation graph for size-4 FFT, optimized.

  test("3") {
    checkOut("3", "scala", {
      val OP: TestFFTC = new TestFFTC with FFTCExp {
        dumpGeneratedCode = true
      }
      val code = utils.captureLocalOut(OP.fft4)
      println(code.replace("compilation: ok", "// compilation: ok"))
      println(OP.fft4(Array(
        1.0,0.0, 1.0,0.0, 2.0,0.0, 2.0,0.0, 1.0,0.0, 1.0,0.0, 0.0,0.0, 0.0,0.0
      )).mkString("// ", ",", ""))
    })

Generated code for FFT4, optimized, as well as sample output. That all the reads are done at the beginning is an artifact of the LMS effect system.

/*****************************************
Emitting Generated Code
*******************************************/
class staged$0 extends ((Array[Double])=>(Array[Double])) {
  def apply(x0:Array[Double]): Array[Double] = {
    val x1 = x0(0)
    val x2 = x0(1)
    val x3 = x0(2)
    val x4 = x0(3)
    val x5 = x0(4)
    val x6 = x0(5)
    val x7 = x0(6)
    val x8 = x0(7)
    val x9 = x1+x5
    val x13 = x3+x7
    val x17 = x9+x13
    val x27 = x0(0)=x17
    val x10 = x2+x6
    val x14 = x4+x8
    val x18 = x10+x14
    val x28 = x0(1)=x18
    val x11 = x1-x5
    val x16 = x4-x8
    val x23 = x11+x16
    val x29 = x0(2)=x23
    val x12 = x2-x6
    val x15 = x3-x7
    val x24 = x12-x15
    val x30 = x0(3)=x24
    val x19 = x9-x13
    val x31 = x0(4)=x19
    val x20 = x10-x14
    val x32 = x0(5)=x20
    val x25 = x11-x16
    val x33 = x0(6)=x25
    val x26 = x12+x15
    val x34 = x0(7)=x26
    x0
  }
}
/*****************************************
End of Generated Code
*******************************************/
// compilation: ok
// 6.0,0.0,-1.0,1.0,0.0,0.0,-1.0,-1.0,1.0,0.0,1.0,0.0,0.0,0.0,0.0,0.0

}
}

Comments? Suggestions for improvement? View this file on GitHub.